TRPO
Created|Updated|IRL
|Post Views:
从动作优势函数说起
首先回顾一下动作优势函数,即:
这里的优势表示的是在状态
援引一张从知乎文章知乎-TRPO中的图: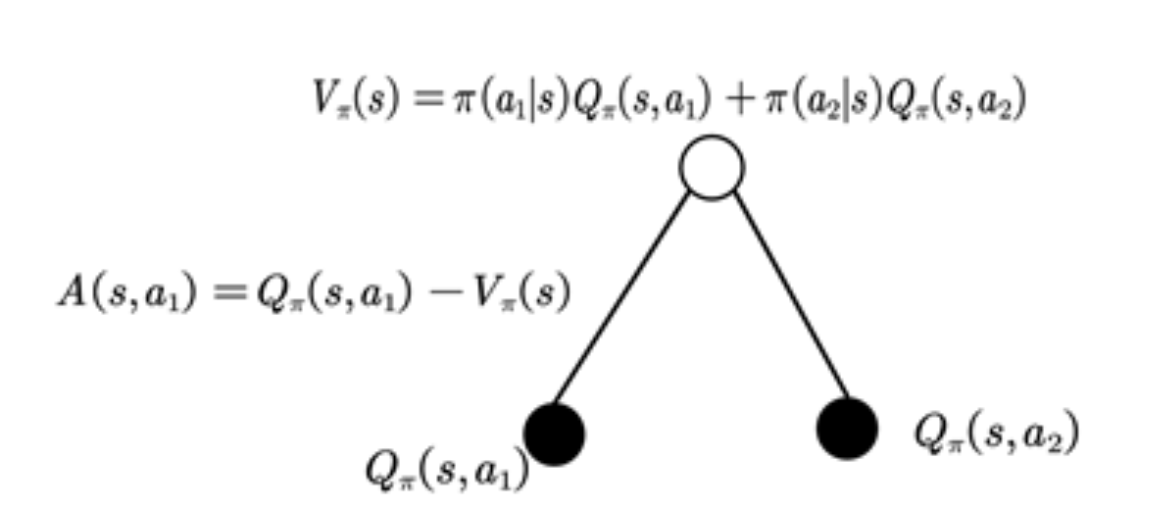
TRPO起始式的推导
TRPO的起点是表达式
这里就给出了在策略
下面来证明这个式子
引入折扣访问频率
定义
那么
最后一步是交换求和顺序,先对
Skill one
TRPO的第一个技巧是,每次更新的策略是临近的,换言之
Author: Eric Li
Copyright Notice: All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.
Related Articles
2024-10-09
GAIL
最大熵逆强化学习的另一种写法这里给出IRL的另一种表述形式,即:这其中的 表示策略 的熵 Hint:中间的 部分可以理解为首先是在确定 的情况下面选择一个策略让 的熵是最大的,然后在这个情况下算出 再真实的专家策略获得的奖励做比较 在学出来这个 之后,再学习出最优策略 的过程是 关于这个式子怎么推导最佳的策略,请看文章 Maximum Entropy Inverse Reinforcement Learning GAIL如果这里的数据量比较小,就会导致过拟合,所以考虑加上一个对于奖励函数 的正则项,即 ,把这个式子变成: 那么这样重建出来的就是及满足了熵正则又不会过拟合 怎么解上面的式子考虑定义一个occupancy measure 为:可以认为这个是策略 下面出现行为-状态对 的概率密度 如果有了这个重建的策略定义为: 经过一通算可以发现,这里最后的优化目标就是找到而带入 occupancy measure...
2024-10-16
RLHF
综述这个方法的基本想法就是,我们在强化学习的过程中,可以引入人来打分,避免训练出来的情况不符合预期,更符合实际情况,其大致的流程是: 符号定义这里相比于传统的强化学习是状态-动作,这里假定的环境是在时间 Agent会从环境中观察到 ,并且会选择一个动作 发送给环境 定义一条轨迹的某个片段是由一系列的观察和动作构成的,即 不同于传统强化学习里面环境直接反馈一个Reward回来,这里假设的是人类能够区分不同轨迹之间的优劣,换言之人类能够给出一个偏序,即判定: 评价一个RLHF的算法定量如果说人类给出评价的标准是基于一个可以定量的价值函数 的,即偏序关系 是由产生的那么最后我们只需要看这个Agent是否按照 RL 的标准最大化了 就可以了 定性如果不是能够清晰量化的评判标准,那么就只能靠人类根据感受进行评判了 关于人类选择的记录这里将人类的一个选择记录为 其中的 ,取值分为如下三种情况: 人类认为某个选择更优,则将对应的 置位为 人类认为两个选择等同,则 将独立采样 人类认为不可分辨则该样本不会出现在数据库中最终把所有的数据放在一个数据库 ...
2024-09-21
Maximum Entropy Inverse Reinforcement Learning 论文阅读
背景知识熵信息熵的定义是其含义是含有信息的多少 符号定义轨迹这里定义轨迹是一组决策中所经过的状态、选择的动作的集合 专家示例定义专家的示例(expert demonstrarion)为 表示遵从专家策略选择的一组轨迹 对于价值函数的表示这篇论文认为,价值函数可以相对每个状态的特征进行线性表示,即对于任意一个状态 都可以找到一个 维的向量 来表征其特征,而对于所有状态,可以用一个共享的k维参数向量 表示,即: 重建的价值函数定义重建的价值函数为:表示在某条轨迹下面,所获取的所有价值函数的总和 在前一个假设下,可以写作: 最大熵方法Partition Function(分区函数)定义即对所有轨迹下的所获得的价值函数之和的指数进行求和(连续的情况下就是积分) MaxEnt Formulation在定义的情况下,最大化 来自知乎的解释参考文献:最大熵逆强化学习(Maximum Entropy Inverse Reinforcement Learning)公式推导与疑惑 - 知乎 (zhihu.com) 最大熵学习的追求是要求以 ...
2024-03-20
Gymnasium Environment Configuration
强化学习环境——gymnasium配置注意,现在已经是2024年了,建议使用最新的gymnasium而不是gym 配置正确的python版本现在是2024年的3月20日,目前的gymnasium不支持python3.12,建议使用conda创建一个3.11的环境: 1conda create -n RL python=3.11 然后进入这个环境中: 1conda activate RL 如果使用的是Windows下的powershell,此时你的终端最前面没有显示例如: 1(RL) xxx@xxx.xxx.xxx.xxx:~ 而是: 1xxx@xxx.xxx.xxx.xxx:~ 的话,建议先运行: 1conda init 然后使用 1conda info 查看一下现在的环境是不是激活成功了 安装gymnasium这里有两个坑,第一个是直接安装 gymnasium 只是装了个白板,里面啥也没有,需要安装的是 gymnasium[atari] 和 gymnasium[accept-rom-license]记住,两个都要装 第二个坑是不知道为什么用conda...
2024-03-21
Tmux 使用简介
tmux简介tmux是链接服务器跑服务的神器,可以在取消链接之后继续运行想要运行的程序 使用流程安装tmux使用 1sudo apt install tmux 即可 新建窗口1tmux new -s NAME 即可创建一个名为name的session,然后在里面运行你的指令即可 然后就可以直接关掉这个链接了 退出窗口如果想要退出当前的tmux session 可以先按下 ctrl + B 然后松开(这个时候没有变化是正常的)然后按下 D 就可以在不终止当前任务的情况下退出了。如果想直接终止这个任务,可以按下 ctrl + B + D 即不松手就行了。 关闭session使用命令 1tmux ls 查看当前在运行的session,使用 1tmux kill-sesion -t NAME 关掉session就可以了 恢复session使用命令 1tmux a -t NAME 可以恢复一个session
2024-03-03
Dynamic Programming
递推表达式通过之前的定义可以得到一个递推版本的DP状态转移方程: 这里的 代表的是 步,具体的含义是可以通过 次 action 到达这个状态。所以上面的更新就是从 步的价值函数去更新 步的价值函数这里的并不是Bellman 方程,只是递推表达式,算法要求是到最后接近满足Bellman方程 注意,这里的更新是和策略 有关的,是在策略确定的情况下,通过更新的方式来确定真正的状态价值函数。 具体的算法如图: 在递推的过程中改进策略在迭代的过程中,如果已知策略 的价值函数 希望知道在某个状态 下选择一个不同于 的动作 是否会带来改善,这种策略的价值为:如果上面的式子的值大于目前的状态价值函数 那么就更新此时的策略为 而由于所有的策略的状态价值函数存在偏序关系,也就是说存在 upper bound 那么就可以利用这一点证明,每次取贪心的策略 即$$\pi’ = \mathop{argmax}a q_\pi(s,a) = \mathop{argmax}a \mathbb E[R{t + 1} + \gamma v_\pi (S{t +1}) | S_t...
Announcement
The blog is now under construction
